In this blog post, I would like to provide a summary of my research paper, “Can Local Additive Explanations Explain Linear Additive Models.” The paper was accepted at the journal track of the European Conference on Machine Learning 2023. The list of all accepted papers can be seen here. You can access the paper in the Data Mining and Knowledge Discovery journal.
TL;DR
We proposed an evaluation measure for local additive explanations called Model-Intrinsic Additive Score (MIAS). Using MIAS, we showed that linear additive explanations such as LIME and KernelSHAP can explain Linear Regression models faithfully. On the other hand, they fail to provide faithful explanations when explaining Logistic Regression and Gaussian Naive Bayes.
Introduction
Local explanations are among the most popular tools of the Explainable Artificial intelligence (xAI) community. Local explanations provide information about the prediction of black-box models for a single instance. Local Model-agnostic Explanations are a category of these techniques that can explain any class of machine learning models. Because of their flexibility, they have become increasingly popular. Even though local explanations come in many representations, counterfactual explanations, or prototypes, the most popular representations of these explanations are feature attribution techniques. For a thorough discussion, see [1].
In feature attribution techniques, each feature receives a real value number that represents its importance to the black-box model’s predicted output. The number of explanation techniques is growing rapidly. In one study [2], the authors have listed 29 explanation techniques.
LIME [3] and KernelSHAP [4] are among the most popular local model-agnostic explanation techniques. Unlike other techniques, they have a unique property called the additivity property:
$$ f(x) = \sum_{j=1}^M \phi_j x_j $$
where the predicted output of black-box model $f$ for instance $x$ is decomposed into an additive sum of feature importance scorse $\phi_j$ and instance feature value $x_j$ where $j=1, …, N$ and $N$ is the number of feature in the dataset.
It is relatively easy to show that these local explanations have large disagreements even in simple datasets. In the Figure below, we can see that LIME and KernelSHAP largely disagree when explaining the prediction of a 99.9% accurate Random Forest model for a test instance on the Iris dataset. The explanations are obtained with respect to the instance predicted class:
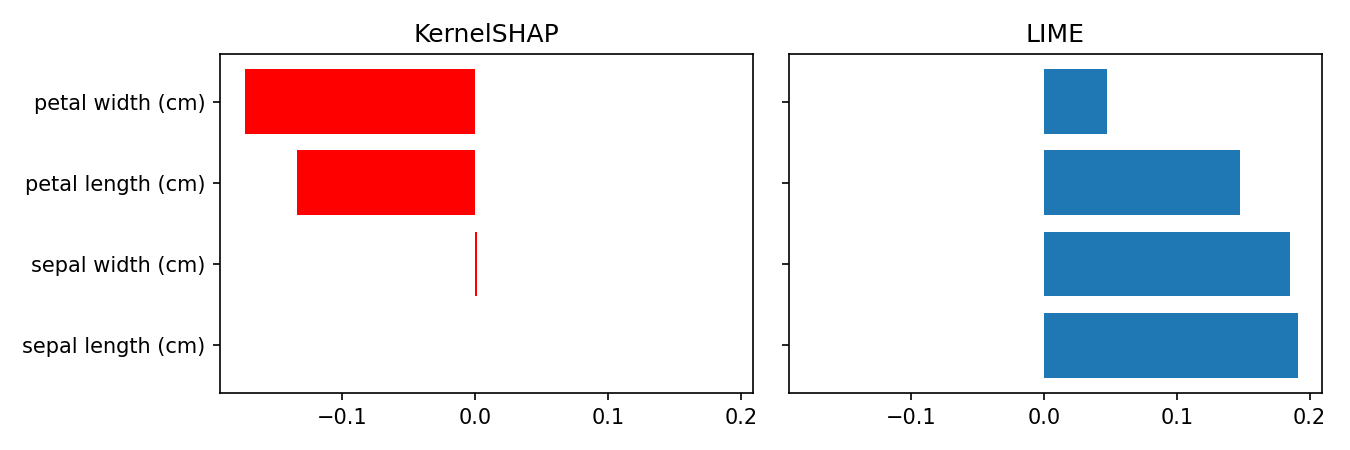
How do we decide which of these explanations is more faithful to the model? Without proper evaluation measures, we cannot conclude that the new explanation techniques are significantly better than their predecessors. In other words, Evaluation is the bottleneck for having more faithful explanations.
Research Question
There are numerous aspects and criteria for which we can evaluate local explanations. One of these aspects is to investigate the additivity property in LIME and KernelSHAP.
We would like to investigate whether the additivity property guarantees that LIME and KernelSHAP can provide faithful explanations for machine learning models that are linear additive.
Related Work
To answer our research question, we need to find a reliable measure for evaluating local explanations. There are numerous evaluation measures for local explanations in the literature. Evaluation techniques for local explanations fall into three main categories:
- Robustness Measures
- Evaluation using Ground Truth from Synthetic Datasets
- Evaluation using Weights of the Logistic Regression
Robustness measures operate by evaluating models using black-box as the oracle. Examples of these measures are Importance by Preservation (Deletion) [5] and (In)fidelity [6]. In the majority of these robustness measures, we evaluate the local explanations by perturbing important (unimportant) features from the explanation in the explained instance. We then measure the change in the predicted score of the black-box model for the instance we explain after this perturbation. Faithful explanations cause large (small) changes in their predicted output of the black-box model for the explained instance.
Evaluation using Ground Truth from Synthetic Datasets [7] extracts ground truth feature importance scores from the datasets that have a polynomial data generation process in the form of $Y = W_0 X_0 + … W_n X_n$. Faithful Local explaantions provide feature importance scores $\Phi$ that are similar to $W = [W_0, W_1, W_2, …, W_n]$ given a similarity metric $d$.
In Evaluation using Weights of the Logistic Regression [8], we explain Logistic Regression. Faithful explanations provide feature importance scores $\Phi$ that are similar to the weights of Logistic Regression $W$ using a similarity metric $d$.
In our study, we are interested in evaluating the ’linear additive’ property of local explanations. None of the available measures in explainability literature is based on this. Therefore, we propose: Model-intrinsic Additive Score (MIAS).
Model-Intrinsic Additive Scores (MIAS)
Let us assume the local explanation technique is linear additive:
$$ f(x) = \sum_{j=1}^M \phi_j x_j $$
If f$ is a linear additive model, we have
$$f(x) = \sum_{j=1}^M \lambda_j x_j $$
In this case, we can calculate the similarity between each additive term in the previous equations. Therefore, we can measure the local explanation accuracy as follows:
$$\sum_{j=1, …, M} d(\phi_j x_j, \lambda_j x_j)$$
where $\lambda_j$ is the linear additive model’s weight for feature $j$ and $d$ is a similarity metric. Based on this, we call $\lambda_j x_j$ a Model-Intrinsic Additive Score (MIAS) for feature $j$. Note that neither local explanations nor linear additive models include interaction terms between features.
We show how MIAS is calculated for Linear Regression and Classification models such as Logistic Regression and Gaussian Naive Bayes.
Linear Regerssion
Model-Intrinsic Additive Scores are directly visible in the Linear Regression models:
$$f(x) = w_0 + \sum_{j=1}^M w_j x_j$$
In this case, we consider $w_j x_j$ as the MIAS score for feature $j$.
Logistic Regression
For Logistic Regression, the prediction function is not linear additive. However, the log odds prediction function is:
$$\text{log} \frac{P(y_n = c | x_n, w )}{P(y_n = \neg c | x_n, w )} = \sum_{m=0}^{M} w^m x_n^m$$
In this case, $\lambda_n^j = w^j x_n^j$ is the Model-Intrinsic Additive Score (MIAS) for feature $j$. Note that for this Evaluation to be fair, we need to explain the log odds ratio function instead of the prediction function $f(x_n). For this, we can pass this function to the explanation techniques instead of the prediction function.
Gaussian Naive Bayes
Similar to the case of Logistic Regression, the prediction function of Naive Bayes is not linear additive. However, the log odds prediction function is:
$$\text{log} \frac{P(y_n = c | x_n)}{P(y_n = \neg c | x_n)} = \sum_{m=1}^{M} \textrm{log} \frac{ \mathcal{N}(x_n^m | \mu_c^m, \sigma_c^m) }{\mathcal{N}(x_n^m | \mu_{\neg c}^m, \sigma_{\neg c}^m)} $$
In this case, the MIAS scores of feature $j$ is $\lambda_n^j = \textrm{log} \frac{ \mathcal{N}(x_n^j | \mu_c^m, \sigma_c^j) }{\mathcal{N}(x_n^j | \mu_{\neg c}^j, \sigma_{\neg c}^j)}$. Similar to the case of Logistic Regression, we need to explain the log odds ratio function in this case.
Empirical Evaluation
We evaluated the local explanations of LIME and KernelSHAP along with Local Permutation Importance (LPI) as a non-additive local explanation over 20 tabular datasets. The idea for including LPI was to investigate whether local additive explanations always outperform local explanations that are not linear or additive. We used Spearman’s rank correlation as our similarity metric and calculated the similarity based on the absolute feature importance scores from MIAS and Local explanations (The argument for this, along with an analysis of the choice of similarity metric, is discussed in detail in our article in Sections 4.5.). We report the average similarity between MIAS and local explanations across all test instances in each dataset. Since we are using a correlation metric for calculating similarity, we consider the average similarity above the threshold of $0.7$ to indicate that local explanations are faithful.
Linear Regression
In the Table below, taken from our paper, we can see the results for explaining Linear Regression models:

We can conclude that in the majority of datasets, LIME and KernelSHAP provide faithful explanations based on MIAS. One interesting pattern is that LPI outperforms LIME and KernelSHAP across many datasets. Therefore, it is shown that local explanations that are linear and additive do not necessarily have an advantage over explanations that are not linear or additive.
Linear Classification
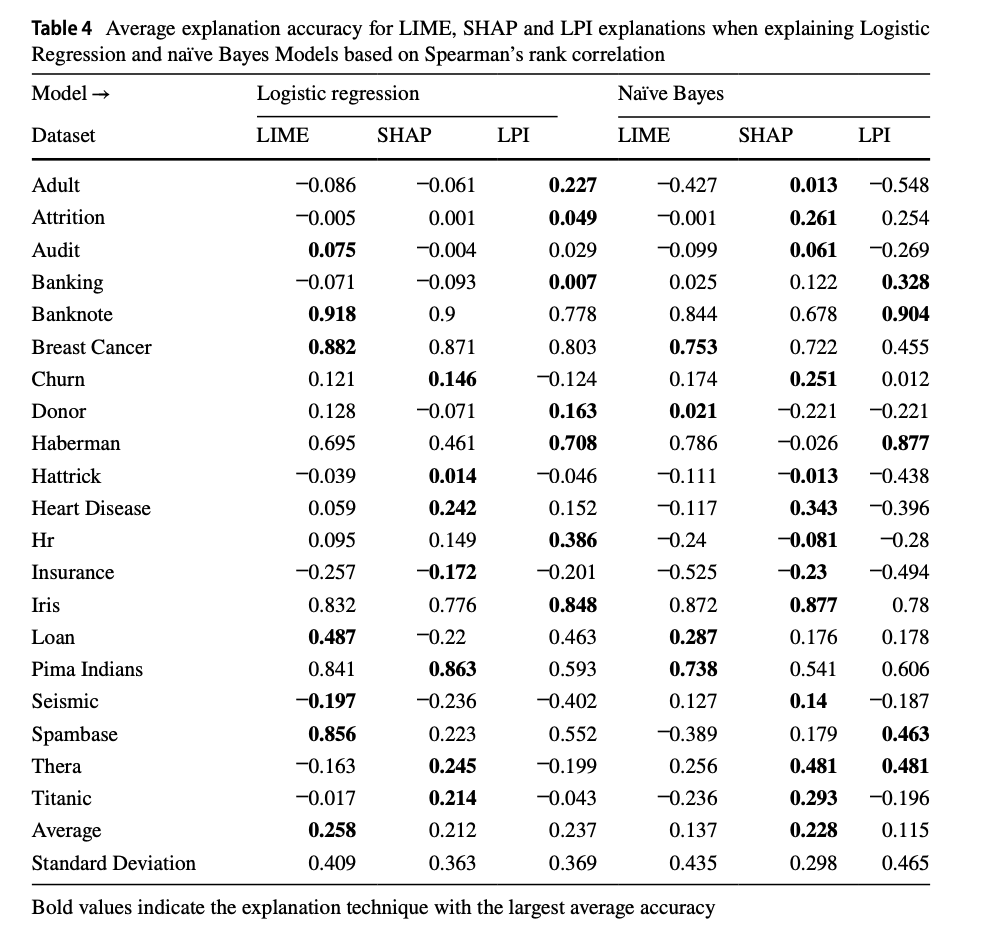
In the Table below, we can see that LIME and SHAP fail to provide faithful explanations based on MIAS across the majority of datasets when explaining Logistic Regression and Naive Bayes models. In some datasets, Churn, Donors, and HR, the similarity of these explanations to MIAS is significantly small. Similar to the previous case, we see that LPI can provide more faithful explanations than LIME and KernelSHAP in numerous datasets, such as Baking, Banknote, and Thera.
Influential Factors
We consider the lack of faithfulness of LIME and KernelSHAP to be surprising. Because of this, we investigate the underlying factors that can affect faithfulness with respect to MIAS at the dataset level, i.e., the average similarity of local explanations to MIAS overall test instances.
In our paper, through extensive experiments using synthetic and tabular datasets, we show that the following factors have a significant influence on the faithful of local explanations using MIAS:
The number of numerical, categorical, and correlated features in the datasets
The test accuracy (Generalization) of the models we explain
The variance in explanation faithfulness within a datasets
The choice of similarity metric
The pre-processing used in the datasets (even when no change in the test accuracy of models is visible)
The results are in Sections 5.2.2 - 5.2.7.
Discussion
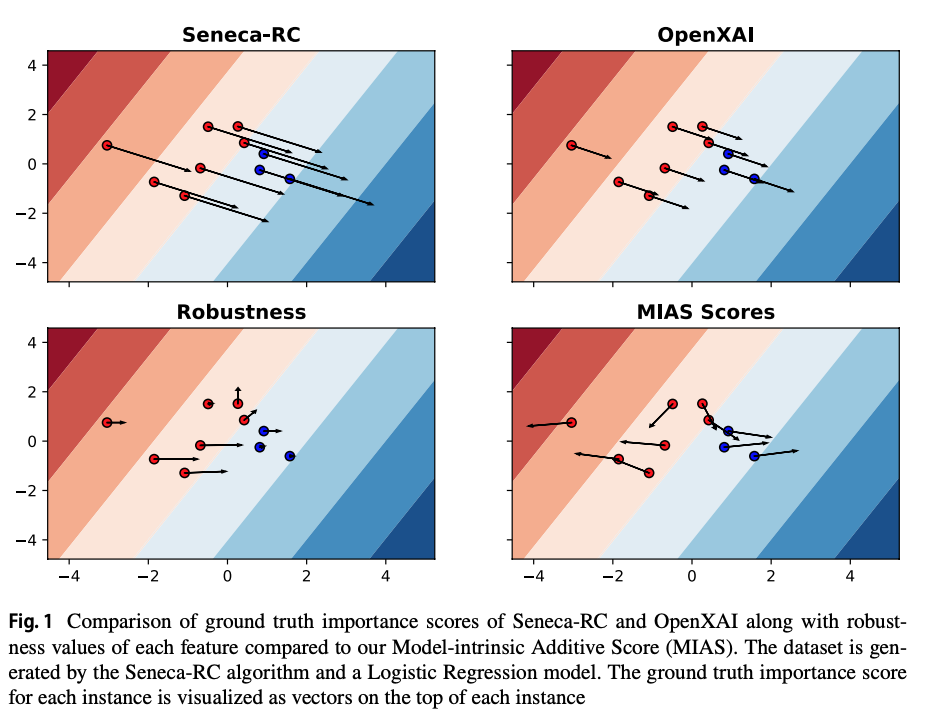
One of the advantages of using MIAS scores for evaluating local explanations is that, unlike other measures, it agree with the decision surface of the linear additive models. In the Figure below, we see the ground truth importance scores of all instances on top of the Logistic Regression decision boundary trained on the synthetic data generation $Y = 2x0 − x1$. The ground truth importance scores are shown on top of each instance based on MIAS and the other related measures [REF].
We can see that MIAS produces different ground truths for instances depending on their position with respect to the decision boundary. Moreover, in all instances, both features play a significant role. Lastly, it is clear that near the decision boundary, MIAS scores are also faithful to the model as the ground truth is noisy, similar to the magnitude of the prediction of Logistic Regression.
MIAS scores also have another advantage compared to other evaluation measures. Unlike other measures, MIAS scores do not suffer from the blame problem. The blame problem is when we blame the explanation wrongfully for their unfaithful explanations when the fault can be traced back to the black-box model as the oracle. We extensively discuss the blame problem in this post.
In our research paper, we also compared the Evaluation using MIAS to other evaluation measures that are mentioned in the related work. The empirical results show that explanations that are faithful with respect to MIAS are not necessarily faithful with respect to other measures, such as robustness measures.
Conclusion
We proposed an evaluation measure for local additive explanations called Model-Intrinsic Additive Score (MIAS). MIAS is extracted based on linear additive terms in the prediction function of linear additive models. We wanted to investigate whether the additive terms of LIME and KernelSHAP can be similar to the additive terms of linear models they explain.
Using MIAS, we showed that LIME and KernelSHAP can explain Linear Regression models faithfully. On the other hand, they fail to provide faithful explanations when explaining Logistic Regression and Gaussian Naive Bayes. Even though LPI is not a linear additive explanation, we showed that it can provide more faithful explanations than LIME and KernelSHAP based on MIAS. We provided a number of factors that can influence the faithfulness of local explanations based on MIAS.
Citation and Code
If you would like to cite our work, you can use the following BibTex:
@article{rahnama2023can,
title={Can local explanation techniques explain linear additive models?},
author={Rahnama, Amir Hossein Akhavan and B{\"u}tepage, Judith and Geurts, Pierre and Bostr{\"o}m, Henrik},
journal={Data Mining and Knowledge Discovery},
pages={1--44},
year={2023},
publisher={Springer}
}
To access the code for our paper, see our Github repo.
References
[1]: Guidotti, Riccardo, et al. “A survey of methods for explaining black box models.” ACM computing surveys (CSUR) 51.5 (2018): 1-42.
[2]: Covert, Ian, Scott Lundberg, and Su-In Lee. “Explaining by removing: A unified framework for model explanation.” Journal of Machine Learning Research 22.209 (2021): 1-90.
[3]: Ribeiro, Marco Tulio, Sameer Singh, and Carlos Guestrin. "" Why should i trust you?" Explaining the predictions of any classifier." Proceedings of the 22nd ACM SIGKDD international conference on knowledge discovery and data mining. 2016.
[4]: Lundberg, Scott M., and Su-In Lee. “A unified approach to interpreting model predictions.” Advances in neural information processing systems 30 (2017).
[5]: Fong, Ruth C., and Andrea Vedaldi. “Interpretable explanations of black boxes by meaningful perturbation.” Proceedings of the IEEE international conference on computer vision. 2017.
[6]: Yeh, Chih-Kuan, et al. “On the (in) fidelity and sensitivity of explanations.” Advances in Neural Information Processing Systems 32 (2019).
[7]: Guidotti, Riccardo. “Evaluating local explanation methods on ground truth.” Artificial Intelligence 291 (2021): 103428.
[8]: Agarwal, Chirag, et al. “Openxai: Towards a transparent evaluation of model explanations.” Advances in Neural Information Processing Systems 35 (2022): 15784-15799.
[9]: Casalicchio, Giuseppe, Christoph Molnar, and Bernd Bischl. “Visualizing the feature importance for black box models.” Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2018, Dublin, Ireland, September 10–14, 2018, Proceedings, Part I 18. Springer International Publishing, 2019.